How to find prime number?
You may remember that a prime number is one whose only factors are itself and 1. Other numbers are called oblong numbers (they can be represented as an oblong of dots) or composite numbers.
Today we examine some shortcuts for finding the prime numbers.
Let’s take 37 for example. Is it prime?
One way is to try each number in turn, from 2 to 37 to see if any of them divide exactly in to 37.
On your calculator this is easy, because the answer to this division calculation would end with “.0” or just show as a whole number. If it shows anything after a decimal point, then it didn’t divide into 37 exactly.
A Shortcut
One shortcut is to realise that if, say, 15 did divide into the number we are testing, then so would 3 and also 5 since 15=3×5. Similarly, if 18 was a factor of the number being tested, since 18=2×9=2x3x3 then 2 would also be a factor and so would 3 (and also 2×3=6 and 3×3=9).
So one shortcut is:
So, instead of checking 2,3,4,5,6,7,… all the way up to 36 to see if 37 is prime, we need only test 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 and 31. But there is another shortcut too:
Another shortcut!
Since 3 is a factor of 18 and 18/3=6, then 18=3×6. We need only test the smaller number, 3, to see if it is a factor of 18 and not 6. Similarly, 5 is a factor 20 and 20=5×4 so we need only test the smaller number 4 as a factor. But what if we don’t know the factors of a number? So, testing a number to see if it is prime means we need only test the “smaller” factors. But where do smaller factors stop and larger factors start? The principle here is:
Suppose one number is a factor of N and that it is smaller than the square-root of the number N. Then the second factor must be larger than the square-root.
We can see this with the examples above: For 18, we need only test numbers up to the square-root of 18 which is 4.243, ie up to 4! This is much quicker than testing all the numbers up to 17!!
For 25, we need to test numbers up to and including the square-root of 25, which is 5.
And for 37, we need only go up to 6 (since 6 x 6=36 so the square-root of 37 will be only a little bit larger).
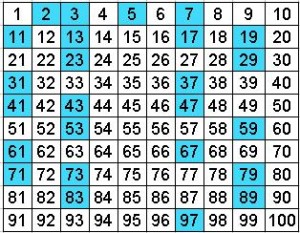
Below we enter prime number from 1 to 100. Blue color boxes indicate prime numbers.
[message_box title=”Program ” color=”red”]
/* Write a program to find Prime number from 1 to N */
/* Written by Utpal Chaudhary */
/*Student of L.D COLLEGE OF ENGINEERING,Ahmedabad-15,Gujarat */
#include <stdio.h>
#include <conio.h>
void main()
{
int num, i=1, j , count;
clrscr();
printf (“Enter Num value To Print Prime Numbers between 1 and Num: “);
scanf (“%d”,&num);
printf (“Prime Numbers upto %d :\n \n”,num);
while(i<=num)
{
count=0;
for(j=1;j<=i;j++)
{
if(i%j==0) //checking whether num is dvisible by j
count++;
}
if(count==2) //if num is divisible by 2 numbers,then it is prime
printf(“%d “,i);
i++;
}
printf(“\n\n”);
getch();
}
[/message_box]
[message_box title=”Output” color=”red”]
Enter Num value To Print Prime Numbers between 1 and Num:45
Prime Numbers upto 45 :
2 3 5 7 11 13 17 19 23 29 31 37 41 43
[/message_box]