Centrifugal Tension
Since the belt continuously runs over the pulleys, therefore, some centrifugal force is caused, whose effect
is to increase the tension on both the tight as well as the slack sides. The tension caused by centrifugal force is called
centrifugal tension. At lower belt speeds (less than 10 m/s), the centrifugal tension is very small, but at higher belt speeds (more than 10 m/s), its effect is considerable and thus should be taken into account.
Consider a small portion PQ of the belt subtending an angle dθ at the centre of the pulley, as shown in Fig. 1.
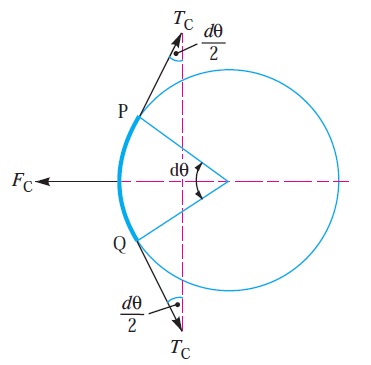
Let m = Mass of belt per unit length in kg,
v = Linear velocity of belt in m/s,
r = Radius of pulley over which the belt runs in metres, and
TC = Centrifugal tension acting tangentially at P and Q in newtons.
We know that length of the belt PQ
= r.dθ
and mass of the belt PQ = m.r.dθ
∴ Centrifugal force acting on the belt PQ,
FC = m.r.dθ × v^2/r
= m.dθ.v^2

The centrifugal tension TC acting tangentially at P and Q keeps the belt in equilibrium. Now resolving the forces (i.e. centrifugal force and centrifugal tension) horizontally, we have
Tc sin (dθ/2) + Tc sin (dθ/2) = Fc = = m.dθ.v^2
Since the angle dθ is very small, therefore putting sin (dθ/2) = (dθ/2) in equation (i), we have
2Tc (dθ/2) = m.dθ.v^2
Tc = m.v^2
Notes : 1. When centrifugal tension is taken into account, then total tension in the tight side,
Tt1 = T1 + Tc
and total tension in the slack side,
Tt2 = T2 + Tc
2. Power transmitted,
P = (Tt1 – Tt2) v …………………….(in watts)
= [(T1 + Tc) – (T2 + Tc)]v = (T1 – T2) v ………………….. (same as before)
Thus we see that the centrifugal tension has no effect on the power transmitted.
3. The ratio of driving tensions may also be written as
2.3 log (Tt1-Tc / Tt2-Tc) = μ.θ
where,
Tt1 = Maximum or total tension in the belt.
Maximum Tension in the Belt
A little consideration will show that the maximum tension in the belt (T ) is equal to the total tension in the tight side of the belt (Tt1).
Let σ = Maximum safe stress,
b = Width of the belt, and
t = Thickness of the belt.
We know that the maximum tension in the belt,
T = Maximum stress × Cross-sectional area of belt
= σ.b.t
When centrifugal tension is neglected, then
T (or Tt1) = T1, i.e. Tension in the tight side of the belt.
When centrifugal tension is considered, then
T (or Tt1) = T1 + Tc
Reference A Textbook of Machine Design by R.S.Khurmi and J.K.Gupta