Introduction to Capacitors
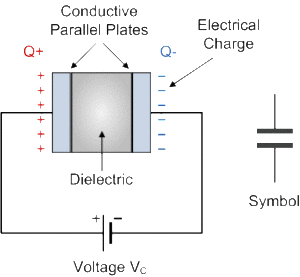
Just like the Resistor, the Capacitor, sometimes referred to as a Condenser, is a simple passive device that is used to “store electricity”. The capacitor is a component which has the ability or “capacity” to store energy in the form of an electrical charge producing a potential difference (Static Voltage) across its plates, much like a small rechargeable battery.
There are many different kinds of capacitors available from very small capacitor beads used in resonance circuits to large power factor correction capacitors, but they all do the same thing, they store charge.
In its basic form, a Capacitor consists of two or more parallel conductive (metal) plates which are not connected or touching each other, but are electrically separated either by air or by some form of a good insulating material such as waxed paper, mica, ceramic, plastic or some form of a liquid gel as used in electrolytic capacitors. The insulating layer between a capacitors plates is commonly called the Dielectric.
Due to this insulating layer, DC current can not flow through the capacitor as it blocks it allowing instead a voltage to be present across the plates in the form of an electrical charge.
The conductive metal plates of a capacitor can be either square, circular or rectangular, or they can be of a cylindrical or spherical shape with the general shape, size and construction of a parallel plate capacitor depending on its application and voltage rating.
When used in a direct current or DC circuit, a capacitor charges up to its supply voltage but blocks the flow of current through it because the dielectric of a capacitor is non-conductive and basically an insulator. However, when a capacitor is connected to an alternating current or AC circuit, the flow of the current appears to pass straight through the capacitor with little or no resistance.
There are two types of electrical charge, positive charge in the form of Protons and negative charge in the form of Electrons. When a DC voltage is placed across a capacitor, the positive (+ve) charge quickly accumulates on one plate while a corresponding negative (-ve) charge accumulates on the other plate. For every particle of +ve charge that arrives at one plate a charge of the same sign will depart from the -ve plate.
Then the plates remain charge neutral and a potential difference due to this charge is established between the two plates. Once the capacitor reaches its steady state condition an electrical current is unable to flow through the capacitor itself and around the circuit due to the insulating properties of the dielectric used to separate the plates.
The flow of electrons onto the plates is known as the capacitors Charging Current which continues to flow until the voltage across both plates (and hence the capacitor) is equal to the applied voltage Vc. At this point the capacitor is said to be “fully charged” with electrons. The strength or rate of this charging current is at its maximum value when the plates are fully discharged (initial condition) and slowly reduces in value to zero as the plates charge up to a potential difference across the capacitors plates equal to the source voltage.
The amount of potential difference present across the capacitor depends upon how much charge was deposited onto the plates by the work being done by the source voltage and also by how much capacitance the capacitor has and this is illustrated below.
Capacitor Construction
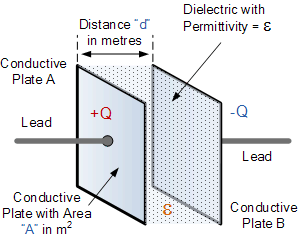
The parallel plate capacitor is the simplest form of capacitor. It can be constructed using two metal or metallised foil plates at a distance parallel to each other, with its capacitance value in Farads, being fixed by the surface area of the conductive plates and the distance of separation between them. Altering any two of these values alters the the value of its capacitance and this forms the basis of operation of the variable capacitors.
Also, because capacitors store the energy of the electrons in the form of an electrical charge on the plates the larger the plates and/or smaller their separation the greater will be the charge that the capacitor holds for any given voltage across its plates. In other words, larger plates, smaller distance, more capacitance.
By applying a voltage to a capacitor and measuring the charge on the plates, the ratio of the charge Q to the voltage V will give the capacitance value of the capacitor and is therefore given as: C = Q/V this equation can also be re-arranged to give the more familiar formula for the quantity of charge on the plates as: Q = C x V
Although we have said that the charge is stored on the plates of a capacitor, it is more correct to say that the energy within the charge is stored in an “electrostatic field” between the two plates. When an electric current flows into the capacitor, charging it up, the electrostatic field becomes more stronger as it stores more energy. Likewise, as the current flows out of the capacitor, discharging it, the potential difference between the two plates decreases and the electrostatic field decreases as the energy moves out of the plates.
The property of a capacitor to store charge on its plates in the form of an electrostatic field is called the Capacitance of the capacitor. Not only that, but capacitance is also the property of a capacitor which resists the change of voltage across it.
The Capacitance of a Capacitor
Capacitance is the electrical property of a capacitor and is the measure of a capacitors ability to store an electrical charge onto its two plates with the unit of capacitance being the Farad (abbreviated to F) named after the British physicist Michael Faraday.
Capacitance is defined as being that a capacitor has the capacitance of One Farad when a charge of One Coulomb is stored on the plates by a voltage of One volt. Capacitance, C is always positive and has no negative units. However, the Farad is a very large unit of measurement to use on its own so sub-multiples of the Farad are generally used such as micro-farads, nano-farads and pico-farads, for example.
Standard Units of Capacitance
- Microfarad (μF) 1μF = 1/1,000,000 = 0.000001 = 10-6 F
- Nanofarad (nF) 1nF = 1/1,000,000,000 = 0.000000001 = 10-9 F
- Picofarad (pF) 1pF = 1/1,000,000,000,000 = 0.000000000001 = 10-12 F
Then using the information above we can construct a simple table to help us convert between pico-Farad (pF), to nano-Farad (nF), to micro-Farad (μF) and to Farads (F) as shown.
| Pico-Farad (pF) | Nano-Farad (nF) | Micro-Farad (μF) | Farads (F) |
| 1,000 | 1.0 | 0.001 | |
| 10,000 | 10.0 | 0.01 | |
| 1,000,000 | 1,000 | 1.0 | |
| 10,000 | 10.0 | ||
| 100,000 | 100 | ||
| 1,000,000 | 1,000 | 0.001 | |
| 10,000 | 0.01 | ||
| 100,000 | 0.1 | ||
| 1,000,000 | 1.0 |
Capacitance of a Parallel Plate Capacitor
The capacitance of a parallel plate capacitor is proportional to the area, A in metres2 of the smallest of the two plates and inversely proportional to the distance or separation, d (i.e. the dielectric thickness) given in metres between these two conductive plates.
The generalised equation for the capacitance of a parallel plate capacitor is given as: C = ε(A/d) where ε represents the absolute permittivity of the dielectric material being used. The permittivity of a vacuum, εo also known as the “permittivity of free space” has the value of the constant 8.84 x 10-12 Farads per metre.
To make the maths a little easier, this dielectric constant of free space, εo, which can be written as: 1/(4π x 9×109), may also have the units of picofarads (pF) per metre as the constant giving: 8.84 for the value of free space. Note though that the resulting capacitance value will be in picofarads and not in farads.
Generally, the conductive plates of a capacitor are separated by some kind of insulating material or gel rather than a perfect vacuum. When calculating the capacitance of a capacitor, we can consider the permittivity of air, and especially of dry air, as being the same value as a vacuum as they are very close.
Capacitance Example No1
A capacitor is constructed from two conductive metal plates 30cm x 50cm which are spaced 6mm apart from each other, and uses dry air as its only dielectric material. Calculate the capacitance of the capacitor.
Then the value of the capacitor consisting of two plates separated by air is calculated as 221pF or 0.221nF
The Dielectric of a Capacitor
As well as the overall size of the conductive plates and their distance or spacing apart from each other, another factor which affects the overall capacitance of the device is the type of dielectric material being used. In other words the “Permittivity” (ε) of the dielectric.
The conductive plates of a capacitor are generally made of a metal foil or a metal film allowing for the flow of electrons and charge, but the dielectric material used is always an insulator. The various insulating materials used as the dielectric in a capacitor differ in their ability to block or pass an electrical charge.
This dielectric material can be made from a number of insulating materials or combinations of these materials with the most common types used being: air, paper, polyester, polypropylene, Mylar, ceramic, glass, oil, or a variety of other materials.
The factor by which the dielectric material, or insulator, increases the capacitance of the capacitor compared to air is known as the Dielectric Constant, k and a dielectric material with a high dielectric constant is a better insulator than a dielectric material with a lower dielectric constant. Dielectric constant is a dimensionless quantity since it is relative to free space.
The actual permittivity or “complex permittivity” of the dielectric material between the plates is then the product of the permittivity of free space (εo) and the relative permittivity (εr) of the material being used as the dielectric and is given as:
Complex Permittivity
In other words, if we take the permittivity of free space, εo as our base level and make it equal to one, when the vacuum of free space is replaced by some other type of insulating material, their permittivity of its dielectric is referenced to the base dielectric of free space giving a multiplication factor known as “relative permittivity”, εr. So the value of the complex permittivity, ε will always be equal to the relative permittivity times one.
Typical units of dielectric permittivity, ε or dielectric constant for common materials are: Pure Vacuum = 1.0000, Air = 1.0006, Paper = 2.5 to 3.5, Glass = 3 to 10, Mica = 5 to 7, Wood = 3 to 8 and Metal Oxide Powders = 6 to 20 etc. This then gives us a final equation for the capacitance of a capacitor as:
One method used to increase the overall capacitance of a capacitor while keeping its size small is to “interleave” more plates together within a single capacitor body. Instead of just one set of parallel plates, a capacitor can have many individual plates connected together thereby increasing the surface area, A of the plates.
For a standard parallel plate capacitor as shown above, the capacitor has two plates, labelled A and B. Therefore as the number of capacitor plates is two, we can say that n = 2, where “n” represents the number of plates.
Then our equation above for a single parallel plate capacitor should really be:
However, the capacitor may have two parallel plates but only one side of each plate is in contact with the dielectric in the middle as the other side of each plate forms the outside of the capacitor. If we take the two halves of the plates and join them together we effectively only have “one” whole plate in contact with the dielectric.
As for a single parallel plate capacitor, n – 1 = 2 – 1 which equals 1, we can mathematically omit this 1 as C = (εo.εr x 1 x A)/d is exactly the same as saying: C = (εo.εr.A)/d which is the standard equation above.
Now suppose we have a capacitor made up of 9 interleaved plates, then n = 9 as shown.
Multi-plate Capacitor
Now we have five plates connected to one lead (A) and four plates to the other lead (B). Then BOTH sides of the four plates connected to lead B are in contact with the dielectric, whereas only one side of each of the outer plates connected to A is in contact with the dielectric. Then as above, the useful surface area of each set of plates is only eight and its capacitance is therefore given as:
Modern capacitors can be classified according to the characteristics and properties of their insulating dielectric:
- Low Loss, High Stability such as Mica, Low-K Ceramic, Polystyrene.
- Medium Loss, Medium Stability such as Paper, Plastic Film, High-K Ceramic.
- Polarized Capacitors such as Electrolytic’s, Tantalum’s.
Voltage Rating of a Capacitor
All capacitors have a maximum voltage rating and when selecting a capacitor consideration must be given to the amount of voltage to be applied across the capacitor. The maximum amount of voltage that can be applied to the capacitor without damage to its dielectric material is generally given in the data sheets as: WV, (working voltage) or as WV DC, (DC working voltage).
If the voltage applied across the capacitor becomes too great, the dielectric will break down (known as electrical breakdown) and arcing will occur between the capacitor plates resulting in a short-circuit. The working voltage of the capacitor depends on the type of dielectric material being used and its thickness.
The DC working voltage of a capacitor is just that, the maximum DC voltage and NOT the maximum AC voltage as a capacitor with a DC voltage rating of 100 volts DC cannot be safely subjected to an alternating voltage of 100 volts. Since an alternating voltage has an r.m.s. value of 100 volts but a peak value of over 141 volts!.
Then a capacitor which is required to operate at 100 volts AC should have a working voltage of at least 200 volts. In practice, a capacitor should be selected so that its working voltage either DC or AC should be at least 50 percent greater than the highest effective voltage to be applied to it.
Another factor which affects the operation of a capacitor is Dielectric Leakage. Dielectric leakage occurs in a capacitor as the result of an unwanted leakage current which flows through the dielectric material.
Generally, it is assumed that the resistance of the dielectric is extremely high and a good insulator blocking the flow of DC current through the capacitor (as in a perfect capacitor) from one plate to the other.
However, if the dielectric material becomes damaged due excessive voltage or over temperature, the leakage current through the dielectric will become extremely high resulting in a rapid loss of charge on the plates and an overheating of the capacitor eventually resulting in premature failure of the capacitor. Then never use a capacitor in a circuit with higher voltages than the capacitor is rated for otherwise it may become hot and explode.
Introduction to Capacitors Summary
We have seen in this tutorial that the job of a capacitor is to store electrical charge onto its plates. The amount of electrical charge that a capacitor can store on its plates is known as its Capacitance value and depends upon three main factors.
- Surface Area – the surface area, A of the two conductive plates which make up the capacitor, the larger the area the greater the capacitance.
- Distance – the distance, d between the two plates, the smaller the distance the greater the capacitance.
- Dielectric Material – the type of material which separates the two plates called the “dielectric”, the higher the permittivity of the dielectric the greater the capacitance.
We have also seen that a capacitor consists of metal plates that do not touch each other but are separated by a material called a dielectric. The dielectric of a capacitor can be air, or even a vacuum but is generally a non-conducting insulating material, such as waxed paper, glass, mica different types of plastics etc. The dielectric provides the following advantages:
- The dielectric constant is the property of the dielectric material and varies from one material to another increasing the capacitance by a factor of k.
- The dielectric provides mechanical support between the two plates allowing the plates to be closer together without touching.
- Permittivity of the dielectric increases the capacitance.
- The dielectric increases the maximum operating voltage compared to air.
Capacitors can be used to block DC current while passing audio signals, pulses, or alternating current, or other time varying wave forms. This ability to block DC currents enables capacitors to be used to smooth the output voltages of power supplies, to remove unwanted spikes from signals that would otherwise tend to cause damage or false triggering of semiconductors or digital components. Capacitors can also be used to adjust the frequency response of an audio circuit, or to couple together separate amplifier stages that must be protected from the transmission of DC current.
At DC a capacitor has infinite impedance (open -circuit), at very high frequencies a capacitor has zero impedance (short-circuit). All capacitors have a maximum working voltage rating, its WV DC so select a capacitor with a rating at least 50% more than the supply voltage.
There are a large variety of capacitor styles and types, each one having its own particular advantage, disadvantage and characteristics. To include all types would make this tutorial section very large so in the next tutorial about The Introduction to Capacitors I shall limit them to the most commonly used types.
